A divisão é a operação que gera mais conflitos de entendimento entre os alunos do ensino fundamental. Muitos estudantes terminam a etapa escolar apresentando muitas dificuldades ou até mesmo sem saber efetuá-la corretamente.
Antes de pensar em estudar o algoritmo da divisão é muito importante que o estudante saiba a tabuada. Sem saber multiplicar, é impossível saber dividir.
Por isso, o estudante precisa saber a tabuada do número que está no divisor desde o 0 até o número 9. Agora, como se efetua uma divisão? Vamos partir de um exemplo simples, em uma primeira etapa:

Foto: depositphotos
1° Exemplo
Thaís tem 25 bonecas e deseja reparti-las igualmente entre suas 5 colegas. Quantas bonecas cada menina irá receber?
Dica: busque solucionar o problema elaborando uma tabela, desta forma trará maior visibilidade para solucionar a questão.
| Número de bonecas | Total | |||||
| Colega 1 | 1 | 1 | 1 | 1 | 1 | 5 |
| Colega 2 | 1 | 1 | 1 | 1 | 1 | 5 |
| Colega 3 | 1 | 1 | 1 | 1 | 1 | 5 |
| Colega 4 | 1 | 1 | 1 | 1 | 1 | 5 |
| Colega 5 | 1 | 1 | 1 | 1 | 1 | 5 |
Desta forma, a divisão poderá ser feita por decomposição:
25 : 5 = (20 : 5) + (5 : 5) = 4 + 1 = 5
2° Exemplo
Em uma excursão de medicina irão 165 médicos distribuídos igualmente em 5 ônibus. Quantos médicos irão em cada ônibus?
165 = 100 + 60 + 5
165 : 5 = (100 : 5) + (60 : 5) + (5 : 5) = 20 + 12 + 1 = 33
33 médicos irão em cada ônibus.
Algoritmo da Divisão: dividendo, divisor, quociente e resto
Nesta segunda etapa vamos nos aprofundar na forma comum de elaborar o posicionamento dos algoritmos da divisão.
A divisão é representada da seguinte forma, temos:
- Dividendo – D (que se pode ou deve dividir);
- Divisor – d (o que divide);
- Quociente – q (resultado da divisão);
- Resto – r (o que sobrou da divisão).
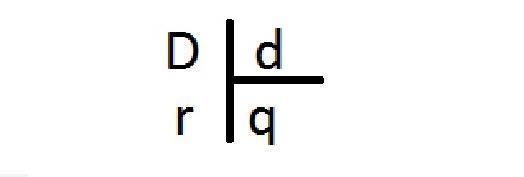
Lembrando que o resto (r) tem que ser sempre menor que o divisor (d): r < d. Por exemplo, se dividirmos o número 7, o resto da divisão (se ele existir) só pode ser: 0, 1, 2, 3, 4, 5 ou 6. Afinal se o resto fosse 7, daria para dividir novamente pelo divisor.
Outro detalhe importante que precisamos saber sobre a divisão é a relação fundamental que diz que: q . d + r = D
3° Exemplo
a) 96 : 4 9 : 4 = 2 dezenas, sobra 1 dezena
96│4 16 : 4 = 4 unidades, 0 resto
16 24
0
| q . d + r = D 24 . 4 + 0 = 96 (20 + 4) . 4 = 96 96 = 96 |
Sendo assim, temos:
q = 24
d = 4
r = 0
D = 96
4° Exemplo
b) 116 : 6
116│6 11 dezenas : 6 = 1 dezena, sobra 5 dezenas
56 019 56 unidades : 6 = 9 unidades, sobra 2 unidades
2
| q . d + r = D 19 . 6 + 2 = 116 (20 – 1) . 6 + 2 = 116 114 + 2 = 116 |




 Informar erro
Informar erro