Área de uma circunferência

Antes de entendermos sobre a área de uma circunferência devemos saber o que é uma circunferência. A circunferência é uma figura que possui o formato todo circular e está mais que presente em diversas situações do nosso dia a dia.

Se olharmos bem a nossa volta perceberemos que o formato circular é muito importante para o funcionamento perfeito de alguns objetos. Temos muito exemplos fáceis e visíveis no nosso cotidiano, as rodas de um carro possui um formato circular, o que facilita a sua locomoção. Outra parte do carro que pode servir de exemplo é o volante que possui esse formato para um melhor controle de direcionamento do carro. Existem vários outros exemplos, as rodas de uma bicicleta, a tampa de uma panela, algumas placas de trânsito, entre outros objetos.

Na área do esporte também percebemos a presença do formato circular, o centro do campo de futebol e de uma quadra de futsal é delimitado por uma circunferência.

A diferença entre o círculo e a circunferência

Muitas pessoas confundem o círculo e a circunferência, porém é muito simples de se perceber qual é a diferença entre os dois.

O círculo é a parte interna da circunferência, enquanto a circunferência é a linha que limita o círculo.

A área de uma circunferência

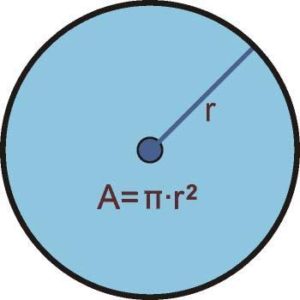
Foto: Reprodução

A circunferência apresenta um elemento que é responsável pela sua área, esse elemento é chamado de raio. O raio é determinado pela distância entre o centro da circunferência e a extremidade.

A expressão da área da circunferência é dada pelo raio e por uma letra grega, o π, essa letra tem o valor de 3,14.

Então a fórmula da área da circunferência é:

A = π. r²

Exemplos de cálculos para descobrir a área de uma circunferência

No primeiro exemplo devemos calcular a área da região onde o raio mede 10 m.

Então teremos:

A = π. r²

A = 3,14 . 10²

A = 3,14 . 100

A = 314 m²

Sendo assim a área dessa circunferência mede 314 m²

No próximo exemplo devemos calcular quantos metros quadrados e grama são necessários para preencher uma praça que possui um formato circular com seu raio medindo 20 metros.

O cálculo que deverá ser feito é o seguinte:

A = π. r²

A = 3,14 . 20²

A = 3,14 . 400

A = 1256 m²

Então será necessário 1256m² de grama.