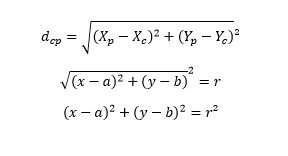Antes de estudarmos a circunferência, precisamos entender algumas definições em torno do assunto.
- Raio: é o segmento de reta que tem como extremidade o centro da circunferência e a outra um ponto qualquer dela.
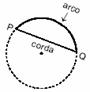
- Arco: é uma parte limitada por dois pontos denominados extremidades do arco.
- Corda: é o segmento de infinitos pontos alinhados que tem como pontos extremos um ponto da circunferência.
- O diâmetro sempre será a maior corda possível, passando pelo centro, tem medida igual a 2r sempre. (d = 2r)
Definição
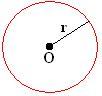
Considerando um ponto “O” de um plano, marcaremos todos os pontos que estão em uma distância igual a “r” Com isso, obtemos a circunferência demonstrada abaixo, cujo centro é “O” e raio “r”.
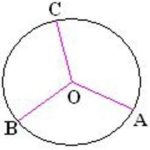
Além disso, qualquer segmento determinado por um ponto da cirtcunferência ao centro é igual ao raio, conforme demonstrado na imagem abaixo. AO = OB = OC = raio
Essa circunferência é chamada de circunferência de centro “O”, e o raio “r” é o conjunto de pontos do plano que distam “r” de “O”.
O diâmetro, por sua vez, é o dobro do valor de um raio, sempre, indo de um lado a outro do círculo, como demonstrado abaixo:
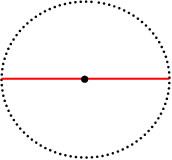
Nesse caso, o comprimento da circunferência é indicado pela linha pontilhada, enquanto o diâmetro pela linha vermelha.
O valor de (pi), por sua vez, pode ser encontrado com a divisão do comprimento pela medida do diâmetro, sendo que é um valor fixo aproximado em 3,14159265.
Características da circunferência
Trata-se, quando falamos de uma circunferência, de um conjunto de pontos de um plano que tenham a distância de um ponto fixo “O” igual à distância “r”. É a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente e, além disso, é simétrica em relação a um número infinito de eixos de simetria.
Equação reduzida
Imagine uma circunferência de centro no ponto C = (a, b) de um plano cartesiano, e P = (x, y) é um ponto qualquer que pertence à circunferência.
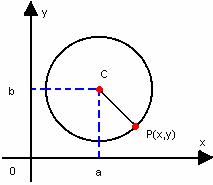
Que propriedades tem o ponto “P”? Sabemos que, pertencendo à circunferência, a distância de “P” até o centro é igual ao raio. Com isso temos que a distância do ponto C = (a, b) a ponto P – (c, y) é igual a R:
(x-a)² + (y-b)² = R
Se elevarmos ao quadrado os dois membros, temos a equação da circunferência de centro (a, b) e raio “R”.




 Informar erro
Informar erro