Função de primeiro grau

Vamos considerar que as letras x e y são variáveis, onde uma depende da outra. Ou seja, para cada valor atribuído a x, existe um valor correspondente para y. Essa dependência é chamada de função, e neste caso y está em função de x, pois é o x quem determina qual será o valor de y.

Foto: Reprodução

Domínio e imagem

O conjunto de valores que é designado para x é chamado de domínio da função, pois é ele quem determina qual será o valor de y. Já os valores de y são chamados de imagem da função, pois eles são ima imagem dos valores de x dentro da função.

Lei de formação

Toda e qualquer função é definida por uma lei de formação, como uma “fórmula” que dita como essa função deve ser formada. No caso da função de 1º grau, a lei de formulação é:

Onde: “a” e “b” são números reais e “a” precisa ser diferente de 0.

Esse tipo de função deve ser resolvida do conjunto dos números reais para o conjunto dos números reais.

Exemplos de funções de primeiro grau

• y = 4x + 2, sendo a = 4 e b = 2;
• y = 5x – 9, sendo a = 5 e b = –9;
• y = – 2x + 10, sendo a = – 2 e b = 10.

Representação gráfica

A função do 1º grau é representada no gráfico através de uma reta. Se pararmos para analisar a lei de formação y = ax + b, podemos notar que além da dependência entre x e y existem mais dois números, a e b.

Esses dois números são os coeficientes da função. O valor de “a”, por exemplo, vai indicar se a função é crescente ou decrescente, enquanto o valor de “b” vai indicar qual é o ponto da reta da função que deve tocar no eixo y do plano cartesiano. Veja melhor na imagem a seguir:

Função crescente                                       Função decrescente

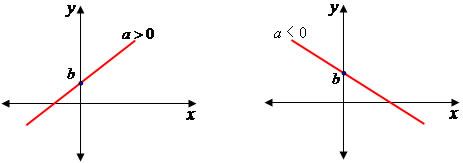
Função crescente e decrescente

Na função crescente, à medida que os valores de x vão aumentando, os valores de y também aumentam. Já na função decrescente existe uma relação inversa: à medida que os valores de x vão aumentando, os valores de y vão diminuindo, e vice versa.

Raiz ou zero de uma função do 1º grau

Quando uma questão nos pede para determinar a raiz ou o zero de uma função, nós precisamos considerar o y = 0. Pelo gráfico nós podemos olhar em que ponto a reta toca no eixo x, tendo y = 0, e ai saberemos qual a raiz da função.