As funções do segundo grau são muito utilizadas em nosso dia a dia, principalmente naquelas situações que estão relacionadas à Física, em que envolvem o movimento uniformemente variado, lançamento oblíquo, em Biologia estudamos essas funções no processo de fotossíntese das plantas e há muitas outras áreas de estudo como Administração, Contabilidade e Engenharia que utilizam essas funções. Conheça um pouco mais sobre elas agora.
Foto: Reprodução
Chamamos de função polinomial do 2º grau, ou de função quadrática, qualquer função f de IR em IR, onde usamos a fórmula f(x) = ax² + bx + c. Nesta, a, b e c são coeficientes reais e a é diferente de zero. Veja agora alguns exemplos dessa função:
1.f(x) = 2x² + 6x + 2, onde a = 2, b = 6 e c = 2
2.f(x) = – 3x² + 3x + 6, onde a = -3, b = 3 e c = 6
3.f(x) = 4x² + 3x + 7, onde a = 4, b = 3 e c = 7
3.f(x) = 2x² + x + 4, onde a = 2, b = 0 e c = 4
Representação geométrica
Podemos representar a função do 2º grau geometricamente. Essa representação é feita através de uma parábola, que de acordo com o sinal do número a (podendo ser positivo ou negativo), pode ter a concavidade voltada para baixo ou para cima. Veja a imagem abaixo:
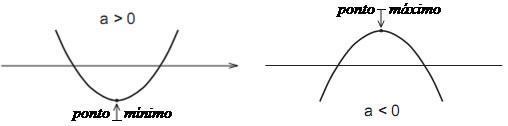
As raízes da função do 2º grau são os pontos em que a parábola toca o eixo x (que é essa reta de segmento).
Concavidade da parábola
Como já foi dito anteriormente, de acordo com o sinal do número a, a parábola pode ter a concavidade voltada para cima ou para baixo. Quando a concavidade está voltada para cima, significa que a > 0, já quando a concavidade está voltada para baixo, indica que a < 0.
Interseção da parábola com o eixo x
A parábola intercepta o eixo x, mais conhecido como o eixo das abscissas, no ponto (x,0), ou seja, sempre que y for igual a zero. Desta forma, temos que: ax² + bx + c = 0. As raízes da função são raízes da equação do 2º grau, ou seja, x = – b ± b2 – 4ac:2a. Que é mais conhecido pela seguinte representação:
![]()
Vértice da parábola
É o vértice da parábola que determina o ponto de mínimo ou de máximo da função. Este será o par ordenado (xv,yv).




 Informar erro
Informar erro