Chamamos de números irracionais aqueles que são apresentados em sua forma decimal. Para ficar mais simples, vamos explicar de outra forma. Os números irracionais são decimais infinitos e não periódicos. São números que possuem infinitas casas decimais, mas atenção: em nenhuma delas encontraremos um período de repetição, como por exemplo: 0,232526 ou 2,354224.
Foto: Reprodução
Números irracionais, números reais e números racionais
Os números irracionais, assim como os reais e racionais, fazem parte dos conjuntos numéricos. Os que são chamados de irracionais são representados pela letra “I” (maiúscula), já aqueles que são reais, são representados pela letra “R” (maiúscula) e, finalmente, os números racionais são representados pela letra “Q” (maiúscula).
Não podem ser representados por fração, por não serrem obtidos através da divisão de dois números inteiros.
O surgimento dos números irracionais
Agora que já entendemos o que são os números irracionais, precisamos entender de onde surgiram. Pitágoras, diante da recusa em aceitar seu problema – que era o cálculo da diagonal de um quadrado, onde o lado mede 1 unidade, diagonal esta que mede √2, dando início ao estudo dos números irracionais – acabou chegando à definição desses números. Confira a imagem abaixo:
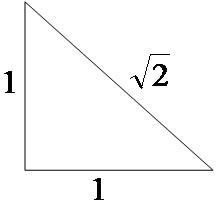
Foto: Reprodução
Os estudos de Pitágoras eram elaborados no ano de 570 a.C. e, obviamente, naquele tempo não existiam calculadoras, de forma que o único mecanismo para encontrar os valores das raízes quadradas envolviam os números quadrados (√2², √3²,…).
O número irracional mais popular: π
A constante π é muito utilizada e de extrema importância para a trigonometria e geometria, mas o que é? O (pi) π, é o número irracional mais conhecido por todos: é um número obtido pela divisão do comprimento de uma circunferência pela medida de seu diâmetro. Independentemente do valor da circunferência de π, este cálculo explicado acima sempre resultará no mesmo valor, que é:
π = 3,1415926535897932384626433832795…
Esse número é, comumente, abreviado em 3 ou 4 casas, podendo ser usado em contas como π= 3,14 ou ainda π=3,141.
Raiz quadrada não exata é um número irracional
Como a maioria de vocês já sabe, todos os números naturais (números inteiros) possuem raiz quadrada. Mas quando alguns números não possuem a raiz quadrada inexata, os nomeamos como números irracionais, como por exemplo:
√2 = 1,4142135623730950488016887242097…
√3 = 1,7320508075688772935274463415059…
Como explicado anteriormente, em números irracionais, nunca descobriremos o valor da última casa decimal, uma vez que esses números são infinitos em suas casas decimais, além de serem não periódicos.




 Informar erro
Informar erro