Quando estudamos matemática aprendemos sobre geometria, e consequentemente sobre os poliedros. Mas você sabe o que são poliedros? Como é sua estrutura e quais as classificações que podem ter? Descubra um pouco mais sobre eles agora mesmo.
Definição
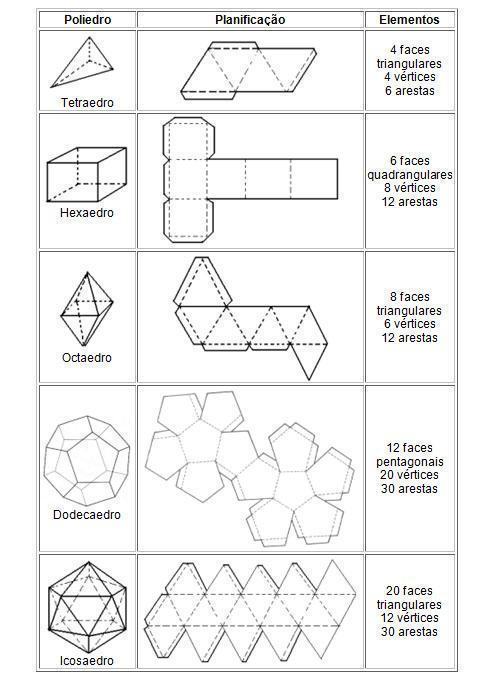
Os poliedros são sólidos geométricos formados por vértices, arestas e faces. Esse sólido é limitado por quatro ou mais polígonos planos que pertencem a planos diferentes e que têm dois a dois somente uma aresta em comum.
Cada face de um poliedro é um polígono, podendo ser triângulos, quadriláteros, pentágonos e muitos outros.
Características
Quando um poliedro possui como faces apenas polígonos regulares, que sejam idênticos e que também apresente todos os ângulos poliédricos idênticos entre si chamamos ele de poliedro regular.
Platão estudou uma classe mais específica de poliedros, que depois vieram a ser chamados de Poliedros de Platão. Estes poliedros se encaixam na classificação de poliedros regulares. São eles: o cubo, o tetraedro, o octaedro, dodecaedro e icosaedro. Veja a imagem deles a seguir:
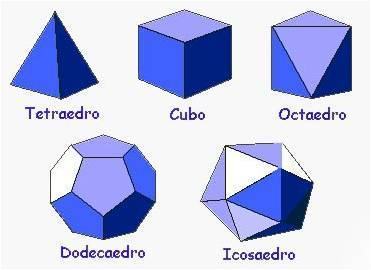
Foto: Reprodução
Um poliedro de Platão deve ter as seguintes características:
- Todas as suas faces devem ser polígonos, independente dos polígonos serem regulares (com todos os lados tendo o mesmo tamanho) ou não.
- Todas as pontas devem ser formadas com o mesmo número de arestas.
- O número de faces de um poliedro deve ser igual ou maior que 3.
Tetraedro, octaedro, icosaedro, hexaedro e dodecaedro são os cinco tipos de polliedro de Platão existentes.
Algumas observações devem ser ditas como: Os poliedros podem ser convexos ou não convexos e não é possível se fazer poliedros regulares em polígonos com 6 ou mais lados.
Poliedros regulares
Um poliedro regular é aquele em que cada face tem o mesmo número de lados e existem também o mesmo número de arestas em cada vértice.
Esses são os 5 poliedros regulares
Teorema de Euler
A seguinte fórmula:
V + F = 2 + A
É utilizada quando temos poliedros com arestas, vértices e faces, sendo estes representados pelas letras A, V e F respectivamente.
Para todos os poliedros convexos essa fórmula é verdadeira.
Os poliedros são estudados desde muitos anos atrás, já foram encontrados registros de cerca de 300 a.C., registros dedicados unicamente para esses sólidos regulares, demonstrando vários cálculos de determinam a razão entre o comprimento da aresta e o raio da esfera circunscrita para cada um.
A soma dos ângulos de todas as faces de um poliedro pode ser encontrada usando a seguinte fórmula:
S = (V – 2) * 4r-
Sendo V o número de vértices e r um ângulo reto.
Já essa próxima fórmula irá nos indicar como achar a soma das medidas dos ângulos das faces de um poliedro convexo, observe:
S = (V – 2).360 –
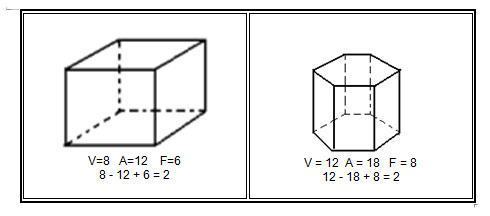
A seguir pode-se observar a relação de Euler na prática:
Em todo poliedro convexo é válida a fórmula seguinte:
V – A + F = 2
em que V é o número de vértices, A é o número de arestas e F, o número de faces.
Observe os exemplos:




 Informar erro
Informar erro